Valentina/11

El simple término “Lógica” es una disciplina que estudia los razonamientos formalmente válidos. La lógica pues se ocupa de la estructura formal de los razonamientos. El contenido expresado en los enunciados queda en un segundo plano. Un razonamiento es formalmente válido si la conclusión se deduce de las premisas que no son otra cosa que las proposiciones representadas por variables proposicionales, por ejemplo: a, b, c, d, e…. Sin embargo, aún conociendo la lógica secuencial de una premisa, muchas veces falta el sentido común para comprenderlo y de ahí la falta de conocimiento que puede envolver a muchos hombres y mujeres en la ignorancia. Según Bernardo Regalado, Jr, la lógica filosófica no es más que ver las realidades de las cosas que pasan a nuestro alrededor y darle un razonamiento profundo y darse cuenta que todo el ser humano en su naturaleza es ignorante porque precisamente ignora muchas cosas.


Por último, según Vlacho, la lógica es ver las cosas por lo que son, más no por lo que aparentan.



En definitiva, la lógica puede definirse como el conjunto de conocimientos que tienen por objeto la enunciación de las leyes que rigen los procesos del pensamiento humano así como los métodos que han de aplicarse al razonamiento y la reflexión para lograr un sistema de raciocinio que conduzca a resultados que puedan considerarse como certeros ó verdaderos.



Debe distinguirse entre la lógica formal y la lógica material :



*La lógica formal (lógica pura) : que es la lógica propiamente dicha es precisamente la “ciencia” (en cuanto a conocimiento) que determina cuáles son las formas correctas y válidas de los raciocinios; pero lo hace considerándolos en sí mismos y con prescindencia de los contenidos concretos de los razonamientos, es decir, considerando esos contenidos como entes lógicos abstractos, de tal manera que las leyes a aplicar tengan validez para cualquier contenido concreto. Por ejemplo: Todo postulado que parta del Teorema de Pitágoras tiene que tener como base lógica y comprobada que: A2 + B2 = C 2. Esto quiere decir, que el raciocinio parte de ciertos conocimientos establecidos( llamados premisas), que conduce a adquirir un conocimiento nuevo (contenido en la conclusión) sin que para ello haya que recurrir a nuevas constataciones u observaciones sensibles distintas ó adicionales a las ya contenidas en las premisas. Así pues, si el Teorema de Pitágoras es la premisa, el nuevo conocimiento sería corroborar matemáticamente que: C2 = C X C ya que al multiplicar éstos dos factores independientes nos dará C2 o sea, C2 = C2 . Este sería el nuevo conocimiento alcanzado que se basó en una conocida premisa. Por lo tanto, la verdad a que conduce la lógica formal, es una verdad formal, que será verdad en tanto sea verdad el contenido de las premisas e indicará solamente que existe una congruencia de ese raciocinio, consigo mismo. Si en un razonamiento existe falsedad en las premisas, la conclusión es falsa y, viceversa. Pero en cualquiera de los casos, será correcto ó válido como razonamiento.



*La lógica material (lógica aplicada) :es aquella en que un proceso de raciocinio ó de pensamiento se analiza en consideración al contenido real de sus premisas, y por lo tanto, debe conducir a una verdad material, ó sea, una conclusión que sea concordante con la realidad. Por ejemplo: La fórmula H 0 es la concreción de un resultado real que todos palpamos y conocemos: el agua, ya que con dos moléculas de hidrógeno y una de oxigeno obtenemos el origen del preciado líquido.



Sin embargo, hay hechos reales que se manejan con normas y pensamientos pre-establecidos por el hombre en sus leyes sociales y civiles como el Derecho donde los escenarios no son todo el tiempo igual. Varían de acuerdo a las circunstancias y los acontecimientos acaecidos. Por lo tanto, las leyes de la lógica formal solamente serán aplicables con especial precaución. De tal manera, las leyes de la lógica formal solamente resultarán aplicables con alcance estricto en el campo de las ciencias puramente exactas y abstractas, tales como las matemáticas, la propia lógica, la mecánica, etc. . Así pues, aquellas disciplinas exclusivamente normativas y abstractas tales como el derecho, la sociología, la psicología, la economía, la administración corresponderán a la lógica no formal, pero que podrán tener efectos y consecuencias materiales relevantes para cualquier sociedad actual, con variables que estarán compuestas de premisas formales ó no formales del pensamiento universal del hombre desde el principio de los tiempos.







Diferencia entre lógica y psicología:

Se dice de la lógica que es el estudio de las leyes del pensamiento. Pero cómo pensamos es también un tema de interés para la psicología, que es una ciencia diferente de la lógica. A la lógica le interesa la claridad y la corrección del pensamiento, no cómo se origina en la mente o qué papel juega dentro de la personalidad de un individuo. Podemos decir que a la psicología le interesa el pensamiento en cuanto es una función de la vida humana concreta. La lógica, en cambio, sólo se preocupa por lo común en el pensamiento, independientemente de quién o quiénes lo tengan en su mente. Por otra parte, no todo pensamiento interesa a la lógica. No le interesa por ejemplo, el pensamiento imaginativo o de "soñar despierto". Le interesa el pensamiento que tiene la forma de proposiciones, es decir, afirmaciones o negaciones de hechos, o bien el que tiene la forma de razonamientos, es decir, pasos de la verdad de unas proposiciones a la verdad de otras. A la lógica no le interesa, pero a la psicología sí, por ejemplo, cómo fue que a un científico se le ocurrió una idea genial. En cambio, a la lógica le interesa muchísimo saber si la idea es coherente, o hasta qué punto podemos considerarla verdadera y por qué. Estas cosas no son de interés para el psicólogo.

PRACTICO.. "LOGICA".. FLORENCIA BOBI

La lógica es una ciencia formal y una rama de la filosofía que estudia los principios de la demostración e inferencia válida. La palabra deriva del griego antiguo λογική (logike), que significa «dotado de razón, intelectual, dialéctico, argumentativo», que a su vez viene de λόγος (logos), «palabra, pensamiento, idea, argumento, razón o principio».

La lógica examina la validez de los argumentos en términos de su estructura, (estructura lógica), independientemente del contenidoespecífico del discurso y de la lengua utilizada en su expresión y de los estados reales a los que dicho contenido se pueda referir.

Esto es exactamente lo que quiere decir que la lógica es una ciencia «formal».

Tradicionalmente ha sido considerada como una parte de la filosofía. Pero en su desarrollo histórico, a partir del final del siglo XIX, y suformalización simbólica ha mostrado su íntima relación con las matemáticas; de tal forma que algunos la consideran como Lógica matemática.

En el siglo XX la lógica ha pasado a ser principalmente la lógica simbólica. Un cálculo definido por unos símbolos y unas reglas de inferencia.¹ Lo que ha permitido un campo de aplicación fundamental en la actualidad: la informática.       

 Diferentes acepciones del término «lógica»                                                                                                                                                                                  1.1 Ciencia argumentativa y propedéutica                                                                                                              1.2 Ciencia del pensar   
1.3 Ciencia formal1.4 La Lógica informal  

 1_

Ciencia argumentativa y propedéutica

El término «lógica», se encuentra en los antiguos peripatéticos y estoicos como una teoría de la argumentación o argumento cerrado;⁶ De este modo la forma argumentativa responde al principio de conocimiento que supone que representa adecuadamente la realidad.⁷ Por ello, sin perder su condición de formalidad, no son formalistas y no acaban de desprenderse de las estructuras propias del lenguaje.³

 2_   

Ciencia del pensar

Gottfried Leibniz (1646-1716).

Los filósofos racionalistas, sin embargo, al situar el origen de la reflexión filosófica en la conciencia, aportaron, a través del desarrollo del análisis como método científico delpensar

       

   3_     

Ciencia formal

En el último tercio del siglo XIX la Lógica va a encontrar su transformación más profunda de la mano de las investigaciones matemáticas y lógicas, junto con el desarrollo de la investigación de las estructuras profundas del lenguaje, la lingüística, convirtiéndose definitivamente en una ciencia formal

    4_   

La Lógica informal

En el lenguaje cotidiano, expresiones como «lógica» o «pensamiento lógico», aporta también un sentido alrededor de un «pensamiento lateral» comparado, haciendo los contenidos de la afirmación coherentes con un contexto, bien sea del discurso o de una teoría de laciencia, o simplemente con las creencias o evidencias transmitidas por la tradición cultural.

                                

        _   

• ¿Diferencias entre psicología y la lógica?

Existe una gran diferencia ya que la psicología corresponde al estudio de sujeto pensante y de los procesos psicológicos reales que ocurren en él, entre los cuales esta también el proceso de pensar. A diferencia de la lógica que se ocupa del pensamiento elaborado y formulado ya que debe estudiar los pensamientos mismos, analizarlos en sus formas, en su estructura, en sus enlaces y demás caracteres que pueden tener, prescindiendo en absoluto del sujeto que pudo haberlos elaborado ..                                                                                                            LA LÓGICA SIMBÓLICA

             

A) Conectores, funciones de verdad y tablas de la verdad

La lógica tiene como objetivo determinar si los enunciados son verdaderos o falsos. Para ello existen varios principios y tablas de la verdad:
-Principio de bivalencia: dice que todo enunciado o es verdadero o es falso, pero no ambas cosas a la vez. Entonces un enunciado tendrá que ser verdadero o falso.
Tablas de la verdad
Cada conector está definido por una tabla de la verdad y le corresponde una función:
-Negación
-Conjunción
-Disyunción



-Condicional
-BicondicionalB) Lógica de enunciados, calculo de juntores

           

1. Deducción

Argumento deductivo
Hay argumentos deductivos y argumentos inductivos, aunque este tópico de esta separación de argumentos no es del todo acertado, en los argumentos deductivos se va de lo general a lo particular, y en los enunciados inductivos es al contrario, de lo particular a lo general.
Pero entre los filósofos no hay unanimidad ni un acuerdo concreto de si existen estos dostipos de argumentos.
Hay dos tipos de deducción, directa e indirecta. Las directas son las cuales en las que las premisas llevan la conclusión de un modo directo y positivo. La indirecta se da cuando los intentos de obtener una conclusión directa no dan resultado, entonces se dan como un rodeo, así:
1º) Suponer de antemano que la conclusión que se desea probar es falsa.
2º) Obtener una contradicción a partir de lo que hemos supuesto anteriormente.
3º) No aceptar o rechazar lo que hemos supuesto, al ver el resultado.
4º) y, como consecuencia de esto último, afirmar ya la conclusión deseada.
Formulación de argumentos. Deductor. Reglas de Inferencia
El modo tradicional para exponer los argumentos consiste en ver primero las premisas y luego la conclusión a la que se desea llegar, ligada a ellas por partículas como: “luego”, “por tanto”, “por consiguiente”, etc. Por ejemplo:
Si suben los salarios, entonces suben los precios;
Si suben los precios, entonces baja el poder adquisitivo de la moneda.
Es así que suben los salarios.
Luego baja el poder adquisitivo de la moneda.
Esto, de una primera forma, se podría representar así:
p q
q r
p
Luego r
Pero los símbolos lógicos representan una palabra o frase, algunos de ellos son:
P, q, r, s, t,… = son letras que representan las frases o palabras de las que están compuestas las premisas y la conclusión.
= éste símbolo significa “si…..entonces”
= éste símbolo significa “y”
V = éste símbolo significa “o”
= éste símbolo significa “si sólo si”
= éste símbolo significa “luego..”
Éstos son los símbolos que más adelante nos encontraremos en complicadas deduccionesen las que, a partir de unas premisas dadas, y de una conclusión también dada, habrá que determinar paso a paso la conclusión.
La lógica deductiva estudia y formula de una manera explícita y rigurosa las reglas de las operaciones deductivas. Estas reglas se llaman, reglas de inferencia.
La primera regla deductiva, desde los estoicos, es la del “modus ponems”:
“si de una hipótesis se sigue una consecuencia y esa hipótesis se da, entonces necesariamente, se da la consecuencia”.
Para formular una regla de inferencia se usan variables de fórmulas y símbolos lógicos. Y el resultado se expresa tras una línea horizontal. Por ejemplo, la representación del modus ponems:
A B
A
B
El resultado de una deducción supone las premisas y también las reglas de inferencia, o sea, que tanto las premisas como las reglas de inferencia son supuestos de la deducción.
Las premisas que nos dan son cosas que nos suponemos que son verdad, pero justificar su veracidad es algo que no entra dentro de la lógica formal. Pero hay otro tipo de supuestos, que son provisionales, que sirven provisionalmente de apoyo durante la deducción, pero que están hasta el final de la deducción.
Una deducción que parte de supuestos iniciales (no subsidiarios), es una deducción hipotética, y una deducción axiomática es la que tiene premisas, que se apoya en supuestos privilegiados, los axiomas. Una deducción axiomática es una demostración.
El cálculo lógico
Es un conjunto de reglas ordenado de manera sistemática.Las operaciones de deducción se efectúan con un conjunto de símbolos y reglas para formar fórmulas, al que se añaden los sistemas de las reglas de inferencia.

                                                      

Trabajo Practico Filosofia "Logica" - Benjamín Fernandez

Si

                Definiciones de Lógica

   Concepto 1

 El sentido ordinaroi de la palabra logica se refiere a lo que es congruente, ordenado, bien estructurado.

lo ilogico es igual a lo incongruente, desordenado, incoherente. Esto se aplica tanto a las personas como a las situaciones y a los pensamientos.

  La palabra lógica nos indica ya en su origen etimológico (Logos) el sentido básico de nuestra ciencia, que se eleva hasta el espíritu y el pensamiento, la razón y la inteligencia. De esta manera definimos nominalmente la lógica: es la ciencia del pensamiento y la razón.

   Existen dos niveles de lógica: 

• La lógica natural: aptitud que todos poseen para pensar en orden, ilación, coherencia.
• La lógica científica: teoría y practica que permiten el perfeccionamiento de la lógica natural.

   Concepto 2

 La lógica es la ciencia que expone las leyes, modos y formas del conocimiento científico. Se trata de una ciencia formal que no tiene contenido, sino que se dedica al estudio de las formas válidas de inferencia. Es decir, se trata del estudio de los métodos y los principios utilizados para distinguir el razonamiento correcto del incorrecto.

  La etimología muestra que el concepto de lógica deriva del latín logĭca, que a su vez proviene del término griego logikós (de logos, “razón” o “estudio”). El filósofo griego Aristóteles fue pionero al utilizar la noción para referirse al estudio de los argumentos como manifestadores de la verdad en la ciencia, y al plantear al silogismo como el argumento válido.

   

   Concepto 3

 La lógica es una ciencia formal y una rama de la filosofía que estudia los principios de la demostración e inferencia válida. La palabra deriva del griego antiguo λογική (logike), que significa «dotado de razón, intelectual, dialéctico, argumentativo», que a su vez viene de λόγος (logos), «palabra, pensamiento, idea, argumento, razón o principio».  

  La lógica examina la validez de los argumentos en términos de su estructura, (estructura lógica), independientemente del contenido específico del discurso y de la lengua utilizada en suexpresión y de los estados reales a los que dicho contenido se pueda referir.

  Esto es exactamente lo que quiere decir que la lógica es una ciencia «formal».

  Tradicionalmente ha sido considerada como una parte de la filosofía. Pero en su desarrollo histórico, a partir del final del siglo XIX, y su formalización simbólica ha mostrado su íntima relación con las matemáticas; de tal forma que algunos la consideran como Lógica matemática.

  En el siglo XX la lógica ha pasado a ser principalmente la lógica simbólica. Un cálculo definido por unos símbolos y unas reglas de inferencia. Lo que ha permitido un campo de aplicación fundamental en la actualidad: la informática.

        

                Lógica y psicología

Lógica y psicología: Existe una gran diferencia entre estas dos ciencias, la relación que pueda existir seria que prescindirían del sujeto que elabora su lógica y su psicología. La diferencia que existe entre ambas ciencias es que la psicología estudia el sujeto pensante y sus procesos psicológicos que ocurren en el estando también el proceso del pensar; mientras que la lógica, como se ha descrito anteriormente, se ocupa del pensamiento elaborado y formulado, ya que estudia los pensamientos mismos, los analiza, los estructura y encadena el enlace que pueden tener dichos pensamientos.

             Diferentes usos de la Lógica

LÓGICA SIMBÓLICA: 

simbolizar un lenguaje es una operación consistente en sustituir -traducirlos signos de ese lenguaje por símbolos.

Para simbolizar utilizaremos las siguientes reglas:

1. Cada uno de los enunciados simples del lenguaje natural se sustituirá

por variables proposicionales, es decir, por letras enunciativas. Por ejemplo:

“Margarita lloraba con el rostro oculto entre las manos”: p

2.- Las expresiones del lenguaje natural tales como “no”, “no es cierto”, “no

es el caso que”, “es falso”, “no es posible”, etc..., se sustituirán por el símbolo “ ¬

”. Por ejemplo: “No la volví a ver más”: ¬p; “No es verdad que no te conozca”: ¬¬

p

3. Las expresiones del lenguaje natural tales como “y”, “ni”, “pero”, “que”,

“e”, “mas”, etc..., se sustituirán por el símbolo “∧”. Por ejemplo: “no puedo

prohibirlo ni puedo tolerarlo”: ¬p ∧ ¬q; “Llegó, vio y venció”: p ∧ q ∧ r; “No es

cierto que me escuches y no hables”: ¬(p ∧ ¬q).

4. Las expresiones del lenguaje natural tales como “o”; “o esto, o lo otro”; “

bien esto, bien lo otro”; “ya esto, ya lo otro”, etc..., se sustituirán por el símbolo

“∨”. Por ejemplo: “o cierras la puerta o pillaré un resfriado”: p ∨ q; “o te callas o no

te escucho”: p ∨ ¬q.5. Las expresiones del lenguaje natural tales como “si... entonces”;

“...luego...”; “...por lo tanto...”; “...en consecuencia...”; “...se infiere...”; “...se

deduce...”, etc..., se sustituirán por el símbolo “→”. Por ejemplo: “Si Joaquín se

levanta a la hora de siempre, llegará tarde”: p → q; “si me invitan, iré”: p → q

6. Las expresiones del lenguaje natural tales como “... si y sólo si...”;

“...equivale a...”; “...es igual a...”; “...vale por...”, etc..., se sustituirán por el símbolo

“↔”. Por ejemplo: “Un pueblo es democrático si y sólo si hay elecciones libres”: p

↔ q; “sólo en el supuesto de que te haya secuestrado tu novia en la segunda

planta, y lo puedas demostrar, podrás entrar tarde a clase”: (p ∧ q) ↔ r; “Podrás

entrar a formar parte de 1º B sólo si no posees alguna enfermedad infectocontagiosa y tienes un excelente sentido del humor”: p ↔ (¬q ∧ r)

   La lógica simbólica tiene un parecido con las matemáticas, no sólo en el uso de símbolos cuasi matemáticos sino también en la presentación de la lógica a la manera de un cálculo y la formulación de reglas a la manera de operaciones; estas reglas rigen el uso de las conectivas, los cuantificadores y demás operadores. El cálculo puede presentarse de manera axiomática, es decir, partiendo de un número finito de axiomas o esquemas de axiomas, reglas de formación y reglas de transformación, además del vocabulario básico; también puede presentarse de acuerdo a otro método diferente del método axiomático, el llamado método de deducción natural, cuyo punto de partida son oraciones básicas, conectivas y reglas para las conectivas. Cuando las oraciones se cuantifican, tenemos reglas para los cuantificadores, y el sistema de estas reglas abarca, como un caso particular, toda la silogística aristotélica; si añadimos reglas de la identidad tenemos el sistema de lógica elemental. La lógica elemental comienza con el estudio de las conectivas y podemos preguntarnos qué unen esas conectivas; pues bien, pueden unir varias cosas. El sistema de las reglas genera un cálculo que puede interpretarse de varias maneras. Un cálculo sin interpretar constituye un sistema formal, un sistema sintáctico que ofrece reglas para manipular, combinar y generar símbolos a partir del vocabulario básico y las reglas. Podemos interpretar esos símbolos como circuitos eléctricos, por ejemplo, y entonces ese sistema tiene su aplicación en la electrónica y la computación. Pueden interpretarse también como oraciones, juicios, proposiciones, enunciados, y esto abre nuevas posibilidades de aplicación. En efecto, puede aplicarse entonces a diversos segmentos de la realidad: a pensamientos o entidades psicológicas, oraciones o entidades lingüísticas, proposiciones o entidades abstractas, a enunciados que hablen acerca de eventos o acontecimientos. Pero la decisión respecto a cómo interpretar esos signos o símbolos no corresponde a la lógica sino a la filosofía de la lógica.

ENUNCIADOS:

En lógica, a veces se entiende por enunciado una oración que puede ser verdadera o falsa, como "está lloviendo", "hace frío" o "Venus es un planeta". En este sentido, los argumentoslógicos se componen de enunciados: las premisas y la conclusión.

La lógica elemental se divide en: lógica de enunciados lógica de predicados Ambas utilizan un lenguaje propio artificial o formalización de un lenguaje natural que permite analizar las proposiciones del lenguaje natural. El cometido de la lógica clásica elemental es determinar si nuestros razonamientos, independientemente de su contenido, son correctos o incorrectos. Por razonamientos (o argumentos) se entiende un conjunto de proposiciones de tal manera que, una de las cuales, denominada conclusión del razonamiento, pueda presentarse como consecuencia de las demás proposiciones, llamadas premisas del razonamiento. En la lógica de enunciados la unidad mínima es el enunciado, es decir, un segmento lingüístico que tiene sentido completo por sí mismo: Esta fiesta es muy divertida Esta fiesta es muy divertida y la música es muy buena Para que un enunciado sea tal, tiene que poder atribuírsele valores de verdad o falsedad. En el caso de las dos oraciones anteriores, la verdad o falsedad habrá de determinarse empíricamente, comprobando si, de hecho, la fiesta es divertida y buena la música. En este caso, además, la dificultad es aún mayor ya que se trata de una afirmación subjetiva. La lógica de enunciados (o lógica proposicional), trata del estudio de la composición de enunciados mediante conectores (y, o, si...entonces, etc.) y se fundamenta en el principio de bivalencia, según el cual, todo enunciado es verdadero o falso, pero nunca ambas cosas a la vez.. Podemos decir, por lo tanto, que la lógica de enunciados se dedica a formalizar las proposiciones dellenguaje natural en un lenguaje simbólico y a definir los conectores, estudiando las leyes de combinación o deducción de los enunciados que las contienen.

En la lógica de predicados se formaliza y estudia la oración atendiendo a los dos términos que la componen: el sujeto y el predicado. La lógica de enunciados o de proposiciones es el nivel más básico de análisis lógico. Se analizan las relaciones que se dan entre los enunciados o las proposiciones; es, pues, una lógica interproposicional, no intraproposicional. En este nivel se simboliza de la misma manera proposiciones o enunciados de contenido tan diferente como: "ahora llueve", "algunos días llueve" o "todos los días llueve". ¿Qué es uno enunciando o una proposición? Una oración declarativa que puede ser verdadera o falsa. Los enunciados dicen de las cosas y, consecuentemente, pueden ser verdaderos o falsos. No son enunciados las expresiones lingüísticas interrogativas, exclamativas o imperativas. Los enunciados o proposiciones pueden ser atómicos o simples, los que no se pueden descomponer en otros; y moleculares o complejos, los que sí se pueden descomponer. Proposición lógica y valores de verdad El valor de verdad de una proposición lógica atómica (o variable proposicional) es, por definición, verdadero o falso (podemos representarlo como V o F). Así el enunciado “llueve” es verdadero si y sólo si está lloviendo en ese momento. Pero si dicho enunciado se considera como proposición lógica atómica, p, entonces puede ser tanto verdadera como falsa. Es una verdad de hecho o contingente, porque tiene los dos posibles valores de verdad, por la propia definición de proposición lógica. El contenido de la relación de un enunciado con lo real no es objeto de la lógica sino de otras ciencias. LÓGICA DIFUSA: La lógica difusa o lógica heuristica se basa en lo relativo de lo observado como posición diferencial. Este tipo de lógica toma dos valores aleatorios, pero contextualizados y referidos entre sí. Así, por ejemplo, una persona que mida 2 metros es claramente una persona alta, si previamente se ha tomado el valor de persona baja y se ha establecido en 1 metro. Ambos valores están contextualizados a personas y referidos a una medida métrica lineal. La lógica difusa se adapta mejor al mundo real en el que vivimos, e incluso puede comprender y funcionar con nuestras expresiones, del tipo "hace mucho calor", "no es muy alto", "el ritmo del corazón está un poco acelerado", etc. La clave de esta adaptación al lenguaje, se basa en comprender los cuantificadores de nuestro lenguaje (en los ejemplos de arriba "mucho", "muy" y "un poco"). En la teoría de conjuntos difusos se definen también las operaciones de unión, intersección, diferencia, negación o complemento, y otras operaciones sobre conjuntos (ver tambiénsubconjunto difuso), en los que se basa esta lógica. LÓGICA PROPOSICIONAL: es un sistema formal diseñado para analizar ciertos tipos de argumentos. En lógica proposicional, las fórmulas representan proposiciones y las conectivas lógicas son operaciones sobre dichas fórmulas, capaces de formar otras fórmulas de mayor complejidad.1 Como otros sistemas lógicos, la lógica proposicional intenta esclarecer nuestra comprensión de la noción de consecuencia lógica para el rango de argumentos que analiza. Considérese el siguiente argumento: Mañana es miércoles o mañana es jueves. Mañana no es jueves. Por lo tanto, mañana es miércoles. Es un argumento válido. Quiere decir que es imposible que las premisas sean verdaderas y la conclusión falsa. Esto no quiere decir que la conclusión sea verdadera. Si las premisas son falsas, entonces la conclusión también podría serlo. Pero si las premisas son verdaderas, entonces la conclusión también lo es. La validez de este argumento no se debe al significado de las expresiones «mañana es miércoles» y «mañana es jueves», porque éstas podrían cambiarse por otras y el argumento permanecer válido. A continuación hay una tabla que despliega todas las conectivas lógicas que ocupan a la lógica proposicional, incluyendo ejemplos de su uso en el lenguaje natural y los símbolos que se utilizan para representarlas. Conectiva Expresión en el lenguaje natural Ejemplo Símbolo en este artículo Símbolos alternativos Negación no No está lloviendo. 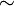Conjunción y Está lloviendo y está nublado.  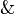. Disyunción o Está lloviendo o está soleado. Condicional material si... entonces Si está soleado, entonces es de día. Bicondicional si y sólo si Está nublado si y sólo si hay nubes visibles. Negación conjunta ni... ni Ni está soleado ni está nublado. 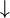Disyunción excluyente o bien... o bien O bien está soleado, o bien está nublado. 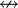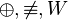En la lógica proposicional, las conectivas lógicas son tratados como funciones de verdad. Es decir, como funciones que toman conjuntos de valores de verdad y devuelven valores de verdad. Por ejemplo, la conectiva lógica no es una función que si toma el valor de verdad V, devuelve F, y si toma el valor de verdad F, devuelve V. Por lo tanto, si se aplica la función noa una letra que represente una proposición falsa, el resultado será algo verdadero. Si es falso que «está lloviendo», entonces será verdadero que «no está lloviendo». Límites de la lógica proposicional La maquinaria de la lógica proposicional permite formalizar y teorizar sobre la validez de una gran cantidad de argumentos. Sin embargo, también existen argumentos que son intuitivamente válidos, pero cuya validez no puede ser probada por la lógica proposicional. Por ejemplo, considérese el siguiente argumento: Todos los hombres son mortales. Sócrates es un hombre. Por lo tanto, Sócrates es mortal. Como este argumento no contiene ninguna de las conectvias «no», «y», «o», etc., según la lógica proposicional, su formalización será la siguiente: p q Por lo tanto, r Pero esta es una forma de argumento inválida, y eso contradice nuestra intuición de que el argumento es válido. Para teorizar sobre la validez de este tipo de argumentos, se necesita investigar la estructura interna de las variables proposicionales. De esto se ocupa la lógica de primer orden. Otros sistemas formales permiten teorizar sobre otros tipos de argumentos. Por ejemplo la lógica de segundo orden, la lógica modal y la lógica temporal. Benjamín Fernandez.